定義問題的類型：以邏輯馬賽克為例

昨晚思想爆走，什麼都不想做的情況下，玩了一下邏輯馬賽克。遊戲規則如下：

• 按左鍵決定該格存不存在方塊。
• 按shift + 左鍵標示該格為空白。
• 點出一幅圖案即完成遊戲。
• 橫軸和縱軸的數字表示該列（行）有多少個方塊，比方第一列寫著135，表示有個三水平長條方塊，長度分別為剛好1、3、5格。

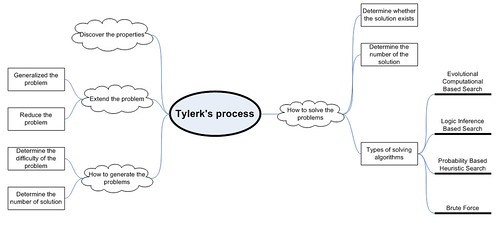
以這樣的遊戲為例，有許多面向可以思考。

依想到的順序條列如下，接著是整理它們之間的關係和重要性：

1. 解題的演算法：暴力搜尋有2^(15*15)種可能，明顯地不可行。玩一陣子後可以找出一些邏輯規則，藉由邏輯推理的必然性，可以整理出推論的演算法，有系統地嘗試。或是引入Heuristic Algorithm，比方用機率分佈猜測各格存在與否的可能性，從最高可能性的組合試起。修過AI Search的話，有許多方法可試。也可以嘗試用演化計算的觀點亂入，應該很有趣。
2. 問題是否有解、是否有唯一解：藉由先畫圖反向推出兩軸的數字，可以發現不見得都是唯一解，也不見得都有解。比方兩軸的數字全是 1 ，會有15!種解。也可以發現問題不見得有解；比方橫軸全是15，縱軸全是0會產生矛盾。於是解題的演算法依解題順序產生兩個子問題：是否有解和有多少組解。也可以將兩者統整為同一問題，無解為 0 組解的特例。
3. 如何產生問題、怎樣才算難的問題：隨機產生圖案再回頭算兩軸的數字為何即可產生問題，但要產生唯一解或困難的問題，得從產生的邏輯組合可能著手，試著由解題演算法反向推出問題困難的模式，像是大數字愈少愈難，從提供數字的組數和大小之間找出困難的平衡，亦可用實驗測試找出可能做法。
4. 減化或延伸問題：定義相似性而決定近似解的優劣；將問題推廣到3維、N維，即對N維空間(d1, d2, …, dn)來說，di為1 ~ k，針對各軸給定數量限制，共有 n*k 組條件，找出符合的分佈方式決定(d1, d2, …, dn)每一點是否存在。原本的問題是n = 2、k = 15的特例。
5. 研究問題的性質：在用n, k描述的一般化問題下，發掘n, k對題目或解法的影響，在什麼條件下會有特殊特性？比方n = 1、k = 1的情況下永遠都是唯一解，不會無解。
6. 統合上述觀點，畫出問題地圖，建立各子問題之間的關係，找出沒看到的問題。亦可針對各個元件決定加入新條件、鬆綁條件會有什麼變化，像鬆綁解的定義就會產生近似解的問題。

偶而做這樣的練習還滿有趣的。最後附上稍微組織過的Mind Map，原本想把上述6項轉為flowchart，做起來不太順，改以Mind Map呈現。